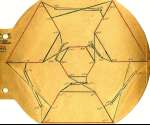
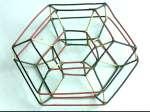
Ringing Shapes
Introduction
These notes relate to work I did in 1968, inspired by some earlier exploration by Tony Walpole, with whom I then worked. I developed the ideas well beyond what Tony had done, built some models of the shapes I had derived, and gave a couple of informal presentations on the work to a handful of interested people at the next Cambridge dinner, and at the 1971 Manchester University Guild dinner. Frank King subsequently used some related ideas to deduce a proof about the possibility of an extent using all triple changes. The work has never been formally written up or published.
(You can skip the theory and look at the pictures .) (If you are unfamiliar with ringing terminology, then look here first .)
The basic concept - Singles (3 bell changes)
A row when ringing is represented as a string of n numbers. So is the position of a point in ndimensional space. In principle therefore, all rows at any stage can be mapped to a unique set of points in the corresponding space, and all allowed changes connecting them can be represented as lines joining the points. On this network it is possible to trace the path of the plain course of a method, any touch of any method, or indeed anything that can be rung within the normal constraints of change ringing (no bell can move more than one place between successive rows). Tony Walpole felt that the resulting shapes should be interesting, and might be useful.
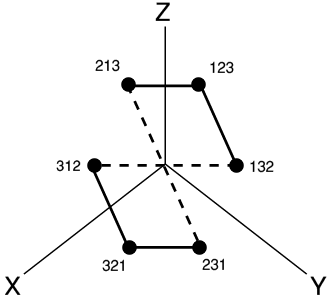 The simple mapping can be done but it is not very productive. Tony plotted the six points corresponding to the six possible rows for Singles (ie the six permutations of three bells). He used the 'obvious' mapping, with the row '123' being represented by the point at the position (1,2,3), and so on. The diagram, right, shows the result. The six points lie at the vertices of a regular hexagon, perpendicular to the line x=y=z, but two of the permitted changes between the rows do not correspond to edges of the hexagon (see dotted lines). This seemed unsatisfactory to Tony, as it did to me when he explained it..
The simple mapping can be done but it is not very productive. Tony plotted the six points corresponding to the six possible rows for Singles (ie the six permutations of three bells). He used the 'obvious' mapping, with the row '123' being represented by the point at the position (1,2,3), and so on. The diagram, right, shows the result. The six points lie at the vertices of a regular hexagon, perpendicular to the line x=y=z, but two of the permitted changes between the rows do not correspond to edges of the hexagon (see dotted lines). This seemed unsatisfactory to Tony, as it did to me when he explained it..
The permitted changes are the transformations that can be produced by swapping adjacent pairs of bells. (This constraint has its origins in the mechanics of how bells are hung and rung. It reduces the energy needed to change the speed of the bell between one row and the next.) Thus the row 123 may change to 213 or to 132, but not to 321. Places are written down in two ways. Pictorially as crosses and lines, eg X1 or 1X, where the X shows a pair of bells crossing between one row and the next, and the I shows a bell staying in the same place. By the number of the place(s) that don't change, eg the above would be '3' and '1' respectively. In the diagram below, the black lines are '1' (1X) and the grey lines are '3' (X1) he lines corresponding to the six permitted changes do not correspond to the edges of the hexagon.
In the diagram, four of the six permitted changes lie around the hexagon, but two cross the middle, giving a distorted figure of eight.
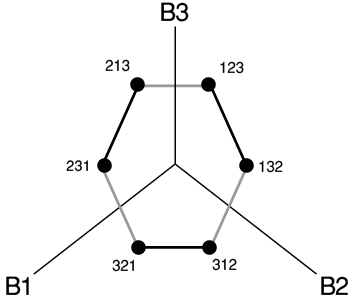 I realised that this 'obvious' mapping was not in fact the best one, because it mixed what I thought of as ordered and non-ordered entities. The places (1st, 2nd, 3rd, etc) are ordered, and this order drives the definition of a permitted change. If only bells in adjacent places can swap, first and last place are different from all the others in that they only have one other place adjacent to them. The bell identities (1, 2, 3, etc) have no such restrictions from a change ringing point of view. Any bell can swap with any other one if they are adjacent in the row. Looking now at the space where the shapes are constructed, the coordinate values, ie the set of distances from the origin parallel to each axis, are ordered like the places, but the axes themselves have no such natural order, and hence the relationship between any pair of axes is similar.
I realised that this 'obvious' mapping was not in fact the best one, because it mixed what I thought of as ordered and non-ordered entities. The places (1st, 2nd, 3rd, etc) are ordered, and this order drives the definition of a permitted change. If only bells in adjacent places can swap, first and last place are different from all the others in that they only have one other place adjacent to them. The bell identities (1, 2, 3, etc) have no such restrictions from a change ringing point of view. Any bell can swap with any other one if they are adjacent in the row. Looking now at the space where the shapes are constructed, the coordinate values, ie the set of distances from the origin parallel to each axis, are ordered like the places, but the axes themselves have no such natural order, and hence the relationship between any pair of axes is similar.
So a better mapping is:
- Place <-> Distance along the axis.
Using this mapping for Singles again produces a hexagon, but now the permitted changes follow its edges, as shown in the second diagram, right. Note that the numbers shown are not conventional co-ordinates, but their inverses. Thus for example the row '231' appears at spatial co-ordinates (3,1,2).
Minimus (4 bell changes)
Minimus maps rows into a four dimensional space, but the resultant shape does not require four dimensions to be shown. Recall that the shape produced for Singles is a flat hexagon, and although it was plotted in a 3-D space, it can be depicted on 2-D surface. Similarly the minimus shape will be a 3-D surface within the 4-D space.
The surface could be plotted numerically, but its structure can be deduced and explained in terms of its components. (Note there are two common notations for changes used in ringing. One just specifies the places made, ie the positions where a bell is not moved by the change. Any place not specified is involved in a swap. Thus '12' means at changes are referred to here by the places made.
There are 24 rows in Minimus ( 4! ) and four allowed changes - three single changes and one double change. Using place notation they are: 12, 14, 34 and X (no places made). In pictorial notation these are respectively IIX, IXI, XII and XX.
Singles is a hexagon, and hexagons will therefore appear in Minimus. There will be a total of eight hexagons. Four represent Singles changes rung on the front three with each of the four different bells in 4ths place. Their edges represent the changes 14 and 34 alternately. The other four hexagons represent Singles being ring on the back three, with each of the four bells in 1st place. Their edges represent the changes 14 and 12 alternately.
Another shape will be present, representing combinations of the changes 12 and 34. This is a square. Its edges represent the changes 12 and 34 alternately, and since these two changes can also occur simultaneously, the squares have diagonal connecting lines that represent the change with no places made (denoted X). There are six squares, since there are six different ways to divide four bells into two pairs.
The table summarises the shapes present:
| Shapes |
Corresponds to ringing |
Places made |
Changes |
Nodes |
Edges |
| 4 Hexagons |
Singles on front 3 |
14 & 34 |
IXI & XII |
24 |
24 |
| 4 Hexagons |
Singles on back 3 |
14 & 12 |
IXI & IIX |
24 |
24 |
6 Squares
with diagonals |
Swapping on front and back pairs
and swapping them together |
12 & 34
and none |
IIX & XII
and XX |
24 |
24 |
| Totals |
|
|
|
72 |
72 |
The complete shape must have 24 nodes (the 24 possible rows), so each node must be shared by 3 shapes (24 =72÷3). From each node must run 3 edges representing the changes (12, 14, 34) ie 72 in total. (The 'X' changes are diagonals, not edges.) Since each edge has a node at each end, there are only 36 distinct edges, and each edge is shared between two hexagons or between a hexagon and a square.
Inspection reveals that the Minimus shape is a truncated octahedron . It is simple to build, colour-code the edges according to the change they represent, and label the nodes with the 24 rows. A plain hunt (alternating changes X and 14) is an equatorial octagon that alternately crosses the diagonal of a square face and runs along the edge between two hexagons. Plain Bob Minimus consists of three such octagons linked by going the opposite way round a hexagon for every 8th move. Plain Bob Minimus is an extent (it generates all 24 possible rows) and so its path visits all 24 nodes once and once only.
By inspection one can find that there are only three paths that visit all nodes using edges only (ie without using the double change 'X'). In ringing terms they are ’Plain Changes’ because they only use single changes. Each of these paths splits the surface into two equal parts that can be folded out flat as shown below. Two are the regular methods Double Court Minimus and Double Canterbury Pleasure Minimus, and one is an un-named irregular method where bells 1 & 2 have one path and bells 3 & 4 have a different path.
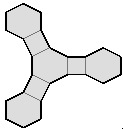
Double Court Minimus |
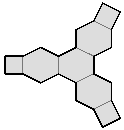
Double Canterbury Pleasure Minimus |
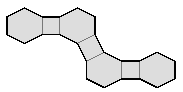
Un-named, irregular
|
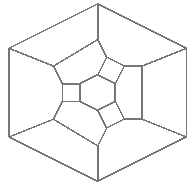 Although Minimus generates a shape that occupies three dimensions, it is in fact a hollow surface that can be distorted and mapped onto a 2-D surface without any edges crossing, as shown right. The outer hexagonal edge and the inner hexagon would be opposite each other in the undistorted shape. This provides a clue that helps with higher dimensions, see below.
Although Minimus generates a shape that occupies three dimensions, it is in fact a hollow surface that can be distorted and mapped onto a 2-D surface without any edges crossing, as shown right. The outer hexagonal edge and the inner hexagon would be opposite each other in the undistorted shape. This provides a clue that helps with higher dimensions, see below.
Doubles (5 bell changes)
Doubles maps rows into a five dimensional space, but the resultant shape can be shown in less than five dimensions. By analogy with Minimus, it will be a 4-D surface within the 5-D space. This is still unhelpful for building a physical model. Recall that the Minimus shape, although occupying 3-D is in fact a surface that can be distorted to fir in 2-D. So we expect the 4-D 'surface' to be capable of mapping into 3-D space, with some distortion, but preserving topological relationships.
We can 'build' this (distorted) shape conceptually by thinking about the components that it must contain. Minimus shapes will be subsets of it, because they represent one bell remaining in either 1st or 5th place, while the others change. By analogy with the inner and outer hexagons of the flattened Minimus shape, we expect to find a Minimus shape at the centre, and another (large) Mimimus shape as its outer bound. Various other shapes will be nested in between, and will connect them together. We can deduce their nature, number and connectedness in the same way as for Minimus. The sub shapes will correspond to different ways of splitting the 5 bells into groups, ie 4+1, 1+4, 3+2 and 2+3.
In the first two groups, four bells change (Minimus) while one remains still in either 1st place or 5th place (like the ones assumed at the centre and outside, but with different bells in 1st and 5th place). So in total there must be:
- 5 truncated octahedrons - Minimus on the front and a bell on the back (one for each bell)
- 5 truncated octahedrons - Minimus on the back and a bell on the front (one for each bell)
In the second two groups, three bells change (Singles) while the remaining bells change and/or stay still. Singles is a Hexagon, and adding the other two bells turn it into a hexagonal prism, with squares (that have diagonals) all the way round. The Singles changing can be in positions 123 or 345, so there must be:
- 10 hexagonal prisms - Singles in 123 and places or changing in 45
- 10 hexagonal prisms - Singles in 345 and places or changing in 12
There are 5!=120 different rows in Doubles, and there are 7 allowed changes: 3 double changes and 4 single changes. In place notation, the double changes are 1, 3, 5 and the single changes 123, 125, 145, 345. In pictorial notation, they are IXX, XIX, XXI and IIIX, IIXI, IXII, XIII. The total number of links is therefore120*7/2 = 420. The double changes are diagonals across squares, so thinking in terms of the solid shapes packed together, there are 4 edges per node, ie a total of 120*4/2 = 240 edges.
The truncated octahedrons each have 24 nodes and 36 edges (excluding diagonals). The hexagonal prisms each have 12 nodes and 18 edges (excluding diagonals). Adding up nodes for all components gives 10*24 + 20*12 = 480 nodes, so with 120 nodes, there must be 4 shapes meeting at each node. Adding up edges for all components gives 10*36 + 20*18 = 720 edges, so with 240 edges, each edge must be shared by 3 component shapes.
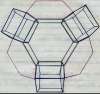 With this information, it is not difficult to deduce the whole structure. Start with a central truncated octahedron. To the 8 hexagonal surfaces, alternately add hexagonal prisms (4) and truncated octahedra (4). On the square faces add further hexagonal prisms edge on (6) oriented to fit against the squares and hexagons of the adjacent truncated octahedra. The way these components fit together can be seen fro the diagram looking out from inside of half a truncated octahedron (Minimus shape). The diagram shows the position and orientation of the hexagonal prisms. The three Minimus shapes attached are not drawn, but they fit against the red hexagons and between the hexagonal faces of the intervening hexagonal prisms. The view out from the other half of the Minimus shape is slightly different. It has three edge-on hexagonal prisms, but what is attached to the hexagons is inverted - the central one is joined to a Minimus shape, and the three around the edges are joined to hexagonal prisms.
With this information, it is not difficult to deduce the whole structure. Start with a central truncated octahedron. To the 8 hexagonal surfaces, alternately add hexagonal prisms (4) and truncated octahedra (4). On the square faces add further hexagonal prisms edge on (6) oriented to fit against the squares and hexagons of the adjacent truncated octahedra. The way these components fit together can be seen fro the diagram looking out from inside of half a truncated octahedron (Minimus shape). The diagram shows the position and orientation of the hexagonal prisms. The three Minimus shapes attached are not drawn, but they fit against the red hexagons and between the hexagonal faces of the intervening hexagonal prisms. The view out from the other half of the Minimus shape is slightly different. It has three edge-on hexagonal prisms, but what is attached to the hexagons is inverted - the central one is joined to a Minimus shape, and the three around the edges are joined to hexagonal prisms.
The sub structure described above, around the central Minimus shape uses half of the available components. Of the remainder, one is a large external truncated octahedron, inside which everything else fits (analogous to te external hexagon in the flattened minimus shapes). The remainder fit between this and the cluster already described, and are identical, apart from an inside-out transformation.
The shape can be built of wire soldered together. It has 420 pieces of wire (including diagonals) and 120 soldered nodes at each of which 7 wires meet - that was a lot of cutting, bending and soldering!
The links represent changes, and can be coloured with a simple code, according to which pairs cross. Single changes will be a single colour, and double changes two (alternating) colours. My model uses:
| Yellow = XIII |
|
Yellow/Grey = XXI |
| Green = IXII |
|
Green/Red = IXX |
| Grey = IIXI |
|
Yellow/Red = XIX |
| Red = IIIX |
|
|
The nodes of the model can be considered to form 5 shells. The inner and outer shells are complete minimus shapes, and correspond to one bell (say bell 1, known as the Treble) being in 1st place and 5th place respectively. It follows that yellow XIII can occur nowhere in the outer shell, because it would move Treble from 1st place. Conversely all the links from this to the 2nd shell must contain yellow to move the Treble out of 1st place (because only 24 rows have it in 1st place). They are yellow XIII, yellow/grey XXI, yellow/red XIX. Therefore all nodes in the second shell represent rows with the Treble in 2nds place. This shell also contains 24 nodes like a complete Minimus shape, but they are not all connected together, because the only changes possible in this shell are IIXI and IIIX. They form disjoint hexagons (ie Singles rung in places 3, 4, 5) each with a different bell in 1st place and the Treble in 2nd place.
The links to the next shell all contain to move the Treble into 3rd place (green IXII, green/red IXX). The third shell is also incomplete, because the only possible changes with the Treble kept in 3rd place are XIII, IIIX and XIX, which just form squares (with diagonals) where pairs of hexagonal prisms share a surface. The links to the 4th shell all contain grey (grey IIXI, yellow/grey XXI). This 4th shell can only contain changes XIII and IXII, which form disjoint hexagons like the 2nd shell.
The links to the 5th, inner, shell contain red to move the Treble into 5th place (red IIIX, green/red IXX, yellow/red XIX). The inner shell, like the outer one, is a complete Minimus shape, with Treble kept in 5th place, and all changes between the other 4 bells to produce the 24 rows.
Of course in terms of the shape, there is nothing unique about the Treble, and the location of two particular Minimus shapes at the 'centre' and 'outside' of the whole Doubles shape is an artefact of the chosen distortion from a 4-D surface to a 3-D shape. The argument above about a colour being absent in a shell and omni-present in the links between shells could be made by distorting the shape to put any other Minimus shape (which has a different bell in 5ths or 1st place) at the 'centre'.
There is another tidy distortion into 3-D. Starting with the flat Minimus shape described above as a base, lay out the other 96 nodes four above each node, to form a total of five layers. These correspond to the shells described above, and are connected in the same way. The top and bottom layers are complete (flat) Minimus shapes. The other minimus shapes and the hexagonal prisms that stand on edge are rather more severely distorted, in some cases having adjacent faces in the same vertical plane.
Despite having shrunk a set of 5-D co-ordinates into a cluster of 3-D shapes, it is in fact possible to go a step (or at least half a step) further. Squashing the stack downwards, the links can be drawn on two sides of a single sheet of card, using the artifice of a few lines (shown double) 'within the thickness of the card'. The holes through the card at the end of these lines line the patterns on the two sides of the card.
Minor (6 bell changes)
Minor maps rows into a six dimensional space, and we have run out of tricks for distorting the result into 3-D. We can though identify the component elements they are:
- 6 Doubles shapes - Doubles on the front and a bell on the back
- 6 Doubles shapes - Doubles on the back and a bell on the front
- 15 concentric truncated octahedral prisms - Minimus on the front and places or changing on the back
- 15 concentric truncated octahedral prisms - Minimus on back and dodging on front
- 20 hexagonal toroids - Singles on the front three and Singles on the back three.)
Each node is joined by 5 single changes, 6 double changes and 1 triple change.
It is possible to describe the shapes surrounding each node in the same way as for Doubles, but modelling the composite shape becomes problematic. Minor is a 5-D surface within a 6-D space. It can be distorted to a 4-D shape, but that is still too much to model in 3-D space without shapes going through each other.
All material copyright © 1968 - 2005 John Harrison
Further reading
If you want a more rigorous mathematical treatment, there is quite a bit of published material, notably by Arthur T White of Western Michigan University, Kalamazoo, USA. For example The Hunting Group. For an overview, and fuller reading list, see Mathematics Library Exhibit: The Mathematics of Change Ringing . Hugh Pumphrey has mapped many different bell ringing methods onto different polyhedra .
You can download a template for building a model of Minimus. See also Maths of ringing .
Pictures
The pictures show the models I built. For simplicity, the diagonals are omitted from all squares in the last two models. Click each image to see a larger picture.
All material Copyright © 1968 - 2007 John Harrison.
 The simple mapping can be done but it is not very productive. Tony plotted the six points corresponding to the six possible rows for Singles (ie the six permutations of three bells). He used the 'obvious' mapping, with the row '123' being represented by the point at the position (1,2,3), and so on. The diagram, right, shows the result. The six points lie at the vertices of a regular hexagon, perpendicular to the line x=y=z, but two of the permitted changes between the rows do not correspond to edges of the hexagon (see dotted lines). This seemed unsatisfactory to Tony, as it did to me when he explained it..
The simple mapping can be done but it is not very productive. Tony plotted the six points corresponding to the six possible rows for Singles (ie the six permutations of three bells). He used the 'obvious' mapping, with the row '123' being represented by the point at the position (1,2,3), and so on. The diagram, right, shows the result. The six points lie at the vertices of a regular hexagon, perpendicular to the line x=y=z, but two of the permitted changes between the rows do not correspond to edges of the hexagon (see dotted lines). This seemed unsatisfactory to Tony, as it did to me when he explained it..  I realised that this 'obvious' mapping was not in fact the best one, because it mixed what I thought of as ordered and non-ordered entities. The places (1st, 2nd, 3rd, etc) are ordered, and this order drives the definition of a permitted change. If only bells in adjacent places can swap, first and last place are different from all the others in that they only have one other place adjacent to them. The bell identities (1, 2, 3, etc) have no such restrictions from a change ringing point of view. Any bell can swap with any other one if they are adjacent in the row. Looking now at the space where the shapes are constructed, the coordinate values, ie the set of distances from the origin parallel to each axis, are ordered like the places, but the axes themselves have no such natural order, and hence the relationship between any pair of axes is similar.
I realised that this 'obvious' mapping was not in fact the best one, because it mixed what I thought of as ordered and non-ordered entities. The places (1st, 2nd, 3rd, etc) are ordered, and this order drives the definition of a permitted change. If only bells in adjacent places can swap, first and last place are different from all the others in that they only have one other place adjacent to them. The bell identities (1, 2, 3, etc) have no such restrictions from a change ringing point of view. Any bell can swap with any other one if they are adjacent in the row. Looking now at the space where the shapes are constructed, the coordinate values, ie the set of distances from the origin parallel to each axis, are ordered like the places, but the axes themselves have no such natural order, and hence the relationship between any pair of axes is similar. 


 Although Minimus generates a shape that occupies three dimensions, it is in fact a hollow surface that can be distorted and mapped onto a 2-D surface without any edges crossing, as shown right. The outer hexagonal edge and the inner hexagon would be opposite each other in the undistorted shape. This provides a clue that helps with higher dimensions, see below.
Although Minimus generates a shape that occupies three dimensions, it is in fact a hollow surface that can be distorted and mapped onto a 2-D surface without any edges crossing, as shown right. The outer hexagonal edge and the inner hexagon would be opposite each other in the undistorted shape. This provides a clue that helps with higher dimensions, see below.