Hexaflexagons
Hexaflexagons are fun to make and play with. There are instructions for making them here . Martin Gardner’s book Mathematical Puzzles and Diversions (Chapter 1) introduced me to them in the late 1960s, and I made several out of paper tape (see also polyhedra and other shapes made from paper tape ). I made a series of three progressively more complex hexaflexagons out of paper tape (tri-hexaflexagon, hexa-hexaflexagon, and dodeca-hexaflexagon).
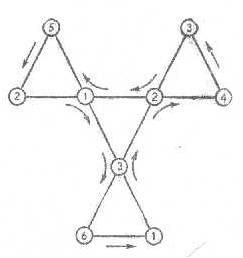 Then I became interested in the diagramatic representation of a Tuckerman Traverse, which is a procedure for cycling through all configurations of any hexaflexagon. The diagram in Martin Gardner’s book, shown here for a hexahexaflexagon, did not seem to have the elegant relationships that I expected from mathematical creations, and while thinking about it I discovered a better approach where continuing the same flex action kept moving in the same direction on the diagram until a boundary was reached, at which point a further flex of the same kind is impossible, So to progress you need to rotate the flexagon 60° and flex it along the other axis. This corresponds to a 120° turn on the diagram. The geometry was the same, but the mapping of points to configurations was diffferent. The notes that I wrote about this at the time are reproduced below.
Then I became interested in the diagramatic representation of a Tuckerman Traverse, which is a procedure for cycling through all configurations of any hexaflexagon. The diagram in Martin Gardner’s book, shown here for a hexahexaflexagon, did not seem to have the elegant relationships that I expected from mathematical creations, and while thinking about it I discovered a better approach where continuing the same flex action kept moving in the same direction on the diagram until a boundary was reached, at which point a further flex of the same kind is impossible, So to progress you need to rotate the flexagon 60° and flex it along the other axis. This corresponds to a 120° turn on the diagram. The geometry was the same, but the mapping of points to configurations was diffferent. The notes that I wrote about this at the time are reproduced below.
When I created this page I assumed someone else must have made the same discovery, but everything I found on the Web used the original diagram. I was beginning to think my ideas were unique when I found Les Pook’s book Flexagons Inside Out . Pook says: ‘Two conventions are possible when laying out a Tuckerman diagram. In the convention used in Fig. 4.8 the cycles are oriented so that if a hexaflexagon is not rotated at a main position then the corresponding direction arrows are in a straight line’, but he doesn’t say who originated this form, or when. His book was published in 2003, 35 years after I wrote my notes. But my idea came 25 years after the Princeton University Flexagon Committee (see: Wikipedia). So I still don’t know whether I was discovering or rediscovering it.
As well as the paper tape hexaflexagons I constructed a large dodecahexaflexagon by sticking together triangular pieces of card with flexible tape hinges, and I then added pictures (each cut into six triangular pieces) on 6 of the resultant 12 faces. The triangles on each face can appear in up to 6 different configurations, only one of which gives the correct image. I distributed these as far as possible from each other on the traverse, with half visible on one side and half on the other side, so although the images appear on 30 of the possible 42 faces visible only 6 of them show the correct images. If I can think of an effective way to combine these images in an interactive model to show how it works then I will do so, but for now there are just the notes I wrote over 50 years ago.
My notes (~1970) with [some interspersed comments].
The diagram showing a Tuckerman Traverse may be profitably modified such that rotation of the flexagon corresponds to a change of direction on the diagram. If this is done, a number of interesting properties appear.
The appearances of any particular face lie around a hexagon, normally incomplete. [In fact they are all incomplete. The outermost ones have only three sides and the others have five sides. This led me to realise somthing else about the diagrams. The progression to higher order hexaflaxagons corresponds to adding an extra triangle to each exposed corner. For the first three (tri- to hexa- to dodeca-) this is possible on a flat piece of paper but for the cositetrahexaflexagon (24 faces) and higher the triangles begin to overlap (though they are not joined to each other) unless distorted to spread them out.] Futher, changes in the form of the face are related to the position on the hexagon.
If a traverse around a hexagon is made (ie changing [both] the direction and corner of flexing at each move) then the face will move from side to side of the flexagon. At each change, the triangles composing the face will suffer a rotation with respect to the centre of the flexagon, and the order of the triangles round the centre will reverse.
Thus the cycle will close in six moves, once round the hexagon. All clockwise arrangements will appear on one side of the flexagon, and all counter clockwise ones on the other. Opposite corners [of the hexagon in the diagram] will be inverses.
A hexagon can never close, but it can overlap, ie it can be an open circuit of more than 6 moves. Overlapping first occurs with 24-hexaflexagons, and with higher numbers, different types of hexagon may be on top of each other.
Any point lies on two hexagons, which determine the two sides of the flexagon in the configuration of the flexagon corresponding to that point.
Traverse diagrams may be formed by starting with a triangle (for a tri-hexaflexagon) and adding a triangle to each free corner for a hexa-hexaflexagon. The process of adding a triangle to each free corner is repeated for each doubling of the order.
To add the notation to a traverse diagram, start with the centre and work out, ie notate the tri-hexa, then the hexa-hexa, and so on. At each stage, the n/2 new numbers must be allocated in a somewhat arbitrary fashion, owing to the the essential symmetry of the situation. At each stage also, rudimentary hexagons will have grown a little, and thus much of the notation is done by extension.
Let variants of the face be x , x’ , x” , x , x’ , x” . It may be convenient to show the inverses by a different colour. No particular significance need be given to which is which. For instance, one may be tempted to say let x -> x’ -> x” be a clockwise sequence. However, this is not possible as adjacent triangles rotate in opposite directions and there is no reason to pick one or the other. As with the choice of numbers, convenience and consistency seem sufficient criteria. The first to be used will be x, the next x’, and then x”. For example, the largest non-overlapping diagram.
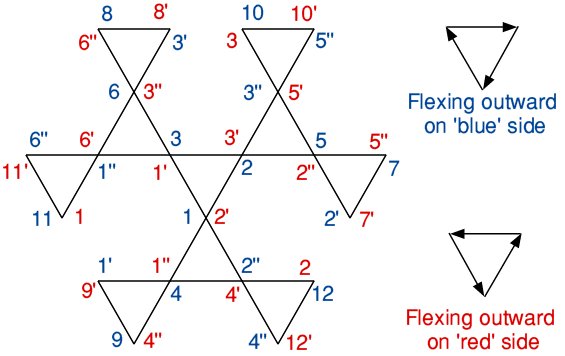
In a Tuckerman traverse a hexaflexagon is only rotated between pinch flexes when this is necessary for flexing to be continued. This guarantees that all possible main positions are visited. It is a useful method of finding the Tuckerman diagram for a hexaflexagon whose dynamic behaviour is unknown. If the hexaflexagon is turned over then the direction of traverse is reversed.
 Then I became interested in the diagramatic representation of a Tuckerman Traverse, which is a procedure for cycling through all configurations of any hexaflexagon. The diagram in Martin Gardner’s book, shown here for a hexahexaflexagon, did not seem to have the elegant relationships that I expected from mathematical creations, and while thinking about it I discovered a better approach where continuing the same flex action kept moving in the same direction on the diagram until a boundary was reached, at which point a further flex of the same kind is impossible, So to progress you need to rotate the flexagon 60° and flex it along the other axis. This corresponds to a 120° turn on the diagram. The geometry was the same, but the mapping of points to configurations was diffferent. The notes that I wrote about this at the time are reproduced below.
Then I became interested in the diagramatic representation of a Tuckerman Traverse, which is a procedure for cycling through all configurations of any hexaflexagon. The diagram in Martin Gardner’s book, shown here for a hexahexaflexagon, did not seem to have the elegant relationships that I expected from mathematical creations, and while thinking about it I discovered a better approach where continuing the same flex action kept moving in the same direction on the diagram until a boundary was reached, at which point a further flex of the same kind is impossible, So to progress you need to rotate the flexagon 60° and flex it along the other axis. This corresponds to a 120° turn on the diagram. The geometry was the same, but the mapping of points to configurations was diffferent. The notes that I wrote about this at the time are reproduced below. 